Las disciplinas de la química han sido agrupadas por la clase de materia bajo estudio o el tipo de estudio realizado. Entre éstas se tienen la química inorgánica, que estudia la materia inorgánica; la química orgánica, que trata con la materia orgánica; la bioquímica, el estudio de substancias en organismos biológicos; la físico-química, comprende los aspectos energéticos de sistemas químicos a escalas macroscópicas, moleculares y atómicas; la química analítica, que analiza muestras de materia tratando de entender su composición y estructura. Otras ramas de la química han emergido en tiempos recientes, por ejemplo, la neuroquímica que estudia los aspectos químicos del cerebro.
La ubicuidad de la química en las ciencias naturales hace que sea considerada como una de las ciencias básicas. La química es de gran importancia en muchos campos del conocimiento, como la ciencia de materiales, la biología, la farmacia, la medicina, la geología, la ingeniería y la astronomía, entre otros.
Los procesos naturales estudiados por la química involucran partículas fundamentales (electrones, protones y neutrones), partículas compuestas (núcleos atómicos, átomos y moléculas) o estructuras microscópicas como cristales y superficies.
Desde el punto de vista microscópico, las partículas involucradas en una reacción química pueden considerarse como un sistema cerrado que intercambia energía con su entorno. En procesos exotérmicos, el sistema libera energía a su entorno, mientras que un proceso endotérmico solamente puede ocurrir cuando el entorno aporta energía al sistema que reacciona. En la gran mayoría de las reacciones químicas hay flujo de energía entre el sistema y su campo de influencia, por lo cual podemos extender la definición de reacción química e involucrar la energía cinética (calor) como un reactivo o producto.
Aunque hay una gran variedad de ramas de la química, las principales divisiones son:
Es común que entre las comunidades académicas de químicos la química analítica no sea considerada entre las subdisciplinas principales de la química y sea vista más como parte de la tecnología química. Otro aspecto notable en esta clasificación es que la química inorgánica sea definida como "química no orgánica". Es de interés también que la Química Física es diferente de la Física Química. La diferencia es clara en inglés: "chemical physics" y "physical chemistry"; en español, ya que el adjetivo va al final, la equivalencia sería:
- Química física
 Physical Chemistry
Physical Chemistry - Física química
 Chemical physics
Chemical physics
La gran importancia de los sistemas biológicos hace que en nuestros días gran parte del trabajo en química sea de naturaleza bioquímica. Entre los problemas más interesantes se encuentran, por ejemplo, el estudio del desdoblamiento de las proteínas y la relación entre secuencia, estructura y función de proteínas.
Si hay una partícula importante y representativa en la química es el electrón. Uno de los mayores logros de la química es haber llegado al entendimiento de la relación entre reactividad química y distribución electrónica de átomos, moléculas o sólidos. Los químicos han tomado los principios de la mecánica cuántica y sus soluciones fundamentales para sistemas de pocos electrones y han hecho aproximaciones matemáticas para sistemas más complejos. La idea de orbital atómico y molecular es una forma sistemática en la cual la formación de enlaces es entendible y es la sofisticación de los modelos iniciales de puntos de Lewis. La naturaleza cuántica del electrón hace que la formación de enlaces sea entendible físicamente y no se recurra a creencias como las que los químicos utilizaron antes de la aparición de la mecánica cuántica. Aún así, se obtuvo gran entendimiento a partir de la idea de puntos de Lewis.
Historia
Las primeras experiencias del hombre como químico se dieron con la utilización del fuego en la transformación de la materia, la obtención de hierro a partir del mineral y de vidrio a partir de arena son claros ejemplos. Poco a poco el hombre se dio cuenta de que otras sustancias también tienen este poder de transformación. Se dedicó un gran empeño en buscar una sustancia que transformara un metal en oro, lo que llevó a la creación de la alquimia. La acumulación de experiencias alquímicas jugó un papel vital en el futuro establecimiento de la química.La química es una ciencia empírica, ya que estudia las cosas por medio del método científico, es decir, por medio de la observación, la cuantificación y, sobre todo, la experimentación. En su sentido más amplio, la química estudia las diversas sustancias que existen en nuestro planeta así como las reacciones que las transforman en otras sustancias. Por otra parte, la química estudia la estructura de las sustancias a su nivel molecular. Y por último, pero no menos importante, sus propiedades.
Subdisciplinas de la química
La química cubre un campo de estudios bastante amplio, por lo que en la práctica se estudia de cada tema de manera particular. Las seis principales y más estudiadas ramas de la química son:[cita requerida]- Química inorgánica: Síntesis y estudio de las propiedades eléctricas, magnéticas y ópticas de los compuestos formados por átomos que no sean de carbono (aunque con algunas excepciones). Trata especialmente los nuevos compuestos con metales de transición, los ácidos y las bases, entre otros compuestos.
- Química orgánica: Síntesis y estudio de los compuestos que se basan en cadenas de carbono.
- Bioquímica: estudia las reacciones químicas en los seres vivos, estudia el organismo y los seres vivos.
- Química física: estudia los fundamentos y bases físicas de los sistemas y procesos químicos. En particular, son de interés para el químico físico los aspectos energéticos y dinámicos de tales sistemas y procesos. Entre sus áreas de estudio más importantes se incluyen la termodinámica química, la cinética química, la electroquímica, la mecánica estadística y la espectroscopía. Usualmente se la asocia también con la química cuántica y la química teórica.
- Química industrial: Estudia los métodos de producción de reactivos químicos en cantidades elevadas, de la manera económicamente más beneficiosa. En la actualidad también intenta aunar sus intereses iniciales, con un bajo daño al medio ambiente.
- Química analítica: estudia los métodos de detección (identificación) y cuantificación (determinación) de una sustancia en una muestra. Se subdivide en Cuantitativa y Cualitativa.
- Química organometálica
- Fotoquímica
- Química cuántica
- Química medioambiental: estudia la influencia de todos los componentes químicos que hay en la tierra, tanto en su forma natural como antropogénica.
- Química teórica
- Química computacional
- Electroquímica
- Química nuclear
- Petroquímica
- Geoquímica: estudia todas las transformaciones de los minerales existentes en la tierra.
- Química macromolecular: estudia la preparación, caracterización, propiedades y aplicaciones de las macromoléculas o polímeros.
- Magnetoquímica
- Química supramolecular
- Nanoquímica
- Astroquímica
Los aportes de célebres autores
Hace aproximadamente cuatrocientos cincuenta y cinco años, sólo se conocían doce elementos. A medida que fueron descubriendo más elementos, los científicos se dieron cuenta de que todos guardaban un orden preciso. Cuando los colocaron en una tabla ordenados en filas y columnas, vieron que los elementos de una misma columna tenían propiedades similares. Pero también aparecían espacios vacíos en la tabla para los elementos aún desconocidos. Estos espacios huecos llevaron al científico ruso Dmitri Mendeléyev a pronosticar la existencia del germanio, de número atómico 32, así como su color, peso, densidad y punto de fusión. Su “predicción sobre otros elementos como - el galio y el escandio - también resultó muy atinada”, señala la obra Chemistry, libro de texto de química editado en 1995.Campo de trabajo: el átomo
El origen de la teoría atómica se remonta a la escuela filosófica de los atomistas, en la Grecia antigua. Los fundamentos empíricos de la teoría atómica, de acuerdo con el método científico, se debe a un conjunto de trabajos hechos por Antoine Lavoisier, Louis Proust, Jeremias Benjamin Richter, John Dalton, Gay-Lussac y Amadeo Avogadro entre muchos otros, hacia principios del siglo XIX.Los átomos son la fracción más pequeña de materia estudiados por la química, están constituidos por diferentes partículas, cargadas eléctricamente, los electrones, de carga negativa; los protones, de carga positiva; los neutrones, que, como su nombre indica, son neutros (sin carga); todos ellos aportan masa para contribuir al peso.
Conceptos fundamentales
Partículas
Los átomos son las partes más pequeñas de un elemento (como el carbono, el hierro o el oxígeno). Todos los átomos de un mismo elemento tienen la misma estructura electrónica (responsable esta de la gran mayoría de las características químicas), pudiendo diferir en la cantidad de neutrones (isótopos). Las moléculas son las partes más pequeñas de una sustancia (como el azúcar), y se componen de átomos enlazados entre sí. Si tienen carga eléctrica, tanto átomos como moléculas se llaman iones: cationes si son positivos, aniones si son negativos.El mol se usa como contador de unidades, como la docena (12) o el millar (1000), y equivale a
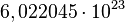 . Se dice que 12 gramos de carbono o un gramo de hidrógeno o 56 gramos de hierro contienen aproximadamente un mol de átomos (la masa molar de un elemento está basada en la masa de un mol de dicho elemento). Se dice entonces que el mol es una unidad de cambio. El mol tiene relación directa con el número de Avogadro. El número de Avogadro fue estimado para el átomo de carbono por el Químico y Físico italiano Carlo Amedeo Avogadro Conde de Quarequa e di Cerreto. Este valor, expuesto anteriormente, equivale al número de partículas presentes en 1 mol de dicha sustancia. Veamos:
. Se dice que 12 gramos de carbono o un gramo de hidrógeno o 56 gramos de hierro contienen aproximadamente un mol de átomos (la masa molar de un elemento está basada en la masa de un mol de dicho elemento). Se dice entonces que el mol es una unidad de cambio. El mol tiene relación directa con el número de Avogadro. El número de Avogadro fue estimado para el átomo de carbono por el Químico y Físico italiano Carlo Amedeo Avogadro Conde de Quarequa e di Cerreto. Este valor, expuesto anteriormente, equivale al número de partículas presentes en 1 mol de dicha sustancia. Veamos:1 mol de glucosa equivale a
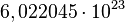 moléculas de glucosa
moléculas de glucosa1 mol de Uranio equivale a
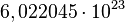 átomos de Uranio
átomos de UranioDentro de los átomos, podemos encontrar un núcleo atómico y uno o más electrones. Los electrones son muy importantes para las propiedades y las reacciones químicas. Dentro del núcleo se encuentran los neutrones y los protones. Los electrones se encuentran alrededor del núcleo. También se dice que es la unidad básica de la materia con características propias. Está formado por un núcleo donde se encuentran protones.
De los átomos a las moléculas
Los enlaces son las uniones entre átomos para formar moléculas. Siempre que existe una molécula es porque ésta es más estable que los átomos que la forman por separado. A la diferencia de energía entre estos dos estados se le denomina energía de enlace.Generalmente, los átomos se combinan en proporciones fijas para dar moléculas. Por ejemplo, dos átomos de hidrógeno se combinan con uno de oxígeno para dar una molécula de agua. Esta proporción fija se conoce como estequiometría.
Orbitales
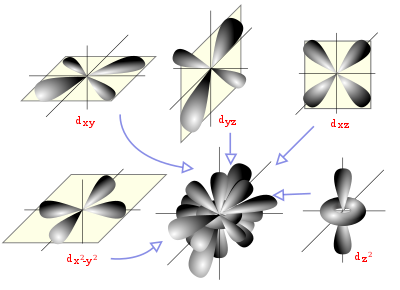
Diagrama espacial mostrando los orbitales atómicos hidrogenoides de momento angular del tipo d (l=2).
Un orbital atómico es una función matemática que describe la disposición de uno o dos electrones en un átomo. Un orbital molecular es análogo, pero para moléculas.
En la teoría del orbital molecular la formación del enlace covalente se debe a una combinación matemática de orbitales atómicos (funciones de onda) que forman orbitales moleculares, llamados así por que pertenecen a toda la molécula y no a un átomo individual. Así como un orbital atómico (sea híbrido o no) describe una región del espacio que rodea a un átomo donde es probable que se encuentre un electrón, un orbital molecular describe una región del espacio en una molécula donde es más factible que se hallen los electrones.
Al igual que un orbital atómico, un orbital molecular tiene un tamaño, una forma y una energía específicos. Por ejemplo, en la molécula de hidrógeno molecular se combinan dos orbitales atómicos uno s ocupados cada uno por un electrón. Hay dos formas en que puede presentarse la combinación de orbitales: aditiva y subtractiva. La combinación aditiva produce la formación de un orbital molecular que tiene menor energía y que tiene, aproximadamente, forma ovalada, mientras que la combinación subtractiva conduce a la formación de un orbital molecular con mayor energía y que genera un nodo entre los núcleos.
De los orbitales a las sustancias
Los orbitales son funciones matemáticas para describir procesos físicos: un orbital solo existe en el sentido matemático, como pueden existir una suma, una parábola o una raíz cuadrada. Los átomos y las moléculas son también idealizaciones y simplificaciones: un átomo sólo existe en vacío, una molécula sólo existe en vacío, y, en sentido estricto, una molécula sólo se descompone en átomos si se rompen todos sus enlaces.En el "mundo real" sólo existen los materiales y las sustancias. Si se confunden los objetos reales con los modelos teóricos que se usan para describirlos, es fácil caer en falacias lógicas.
Disoluciones
En agua, y en otros disolventes (como la acetona o el alcohol), es posible disolver sustancias, de forma que quedan disgregadas en las moléculas o iones que las componen (las disoluciones son transparentes). Cuando se supera cierto límite, llamado solubilidad, la sustancia ya no se disuelve, y queda, bien como precipitado en el fondo del recipiente, bien como suspensión, flotando en pequeñas partículas (las suspensiones son opacas o traslúcidas).Se denomina concentración a la medida de la cantidad de soluto por unidad de cantidad de disolvente.
Medida de la concentración
La concentración de una disolución se puede expresar de diferentes formas, en función de la unidad empleada para determinar las cantidades de soluto y disolvente. Las más usuales son:- g/l (Gramos por litro) razón soluto/disolvente o soluto/disolución, dependiendo de la convención
- % p/p (Concentración porcentual en peso) razón soluto/disolución
- % V/V (Concentración porcentual en volumen) razón soluto/disolución
- M (Molaridad) razón soluto/disolución
- N (Normalidad) razón soluto/disolución
- m (molalidad) razón soluto/disolvente
- x (fracción molar)
- ppm (Partes por millón) razón soluto/disolución
Acidez
El pH es una escala logarítmica para describir la acidez de una disolución acuosa. Los ácidos, como el zumo de limón y el vinagre, tienen un pH bajo (inferior a 7). Las bases, como la sosa o el bicarbonato de sodio, tienen un pH alto (superior a 7).El pH se calcula mediante la siguiente ecuación:
 es la actividad de iones hidrógeno en la solución, la que en soluciones diluidas es numéricamente igual a la molaridad de iones Hidrógeno
es la actividad de iones hidrógeno en la solución, la que en soluciones diluidas es numéricamente igual a la molaridad de iones Hidrógeno ![[H^+]\,](http://upload.wikimedia.org/wikipedia/es/math/1/e/f/1ef3bcce90c20f8119eebc5d3fa164a5.png) que cede el ácido a la solución.
que cede el ácido a la solución.- una solución neutral (agua ultra pura) tiene un pH de 7, lo que implica una concentración de iones hidrógeno de 10-7 M
- una solución ácida (por ejemplo, de ácido sulfúrico)tiene un pH < 7, es decir que la concentración de iones hidrógeno es mayor que 10-7 M
- una solución básica (por ejemplo, de hidróxido de potasio) tiene un pH > 7, o sea que la concentración de iones hidrógeno es menor que 10-7 M
Formulación y nomenclatura
La IUPAC, un organismo internacional, mantiene unas reglas para la formulación y nomenclatura química. De esta forma, es posible referirse a los compuestos químicos de forma sistemática y sin equívocos.Mediante el uso de fórmulas químicas es posible también expresar de forma sistemática las reacciones químicas, en forma de ecuación química. Por ejemplo:
![pH= -\log a_{H^+} \approx -\log [H^+]\,](http://upload.wikimedia.org/wikipedia/es/math/a/c/4/ac4dad8f18c628b37c90eccb2bb4b8cb.png)

