sábado, 19 de noviembre de 2011

LA QUIMICA

Se denomina química (del árabe kēme (kem, كيمياء), que significa "tierra") a la ciencia que estudia la composición, estructura y propiedades de la materia, como los cambios que ésta experimenta durante las reacciones químicas y su relación con la energía. Históricamente la química moderna es la evolución de la alquimia tras la Revolución química (1733).
Las disciplinas de la química han sido agrupadas por la clase de materia bajo estudio o el tipo de estudio realizado. Entre éstas se tienen la química inorgánica, que estudia la materia inorgánica; la química orgánica, que trata con la materia orgánica; la bioquímica, el estudio de substancias en organismos biológicos; la físico-química, comprende los aspectos energéticos de sistemas químicos a escalas macroscópicas, moleculares y atómicas; la química analítica, que analiza muestras de materia tratando de entender su composición y estructura. Otras ramas de la química han emergido en tiempos recientes, por ejemplo, la neuroquímica que estudia los aspectos químicos del cerebro.
La ubicuidad de la química en las ciencias naturales hace que sea considerada como una de las ciencias básicas. La química es de gran importancia en muchos campos del conocimiento, como la ciencia de materiales, la biología, la farmacia, la medicina, la geología, la ingeniería y la astronomía, entre otros.
Los procesos naturales estudiados por la química involucran partículas fundamentales (electrones, protones y neutrones), partículas compuestas (núcleos atómicos, átomos y moléculas) o estructuras microscópicas como cristales y superficies.
Desde el punto de vista microscópico, las partículas involucradas en una reacción química pueden considerarse como un sistema cerrado que intercambia energía con su entorno. En procesos exotérmicos, el sistema libera energía a su entorno, mientras que un proceso endotérmico solamente puede ocurrir cuando el entorno aporta energía al sistema que reacciona. En la gran mayoría de las reacciones químicas hay flujo de energía entre el sistema y su campo de influencia, por lo cual podemos extender la definición de reacción química e involucrar la energía cinética (calor) como un reactivo o producto.
Aunque hay una gran variedad de ramas de la química, las principales divisiones son:
Es común que entre las comunidades académicas de químicos la química analítica no sea considerada entre las subdisciplinas principales de la química y sea vista más como parte de la tecnología química. Otro aspecto notable en esta clasificación es que la química inorgánica sea definida como "química no orgánica". Es de interés también que la Química Física es diferente de la Física Química. La diferencia es clara en inglés: "chemical physics" y "physical chemistry"; en español, ya que el adjetivo va al final, la equivalencia sería:
  • Química física \Longleftrightarrow \; Physical Chemistry
  • Física química \Longleftrightarrow \; Chemical physics
Usualmente los químicos son educados en términos de físico-química (Química Física) y los físicos trabajan problemas de la física química.
La gran importancia de los sistemas biológicos hace que en nuestros días gran parte del trabajo en química sea de naturaleza bioquímica. Entre los problemas más interesantes se encuentran, por ejemplo, el estudio del desdoblamiento de las proteínas y la relación entre secuencia, estructura y función de proteínas.
Si hay una partícula importante y representativa en la química es el electrón. Uno de los mayores logros de la química es haber llegado al entendimiento de la relación entre reactividad química y distribución electrónica de átomos, moléculas o sólidos. Los químicos han tomado los principios de la mecánica cuántica y sus soluciones fundamentales para sistemas de pocos electrones y han hecho aproximaciones matemáticas para sistemas más complejos. La idea de orbital atómico y molecular es una forma sistemática en la cual la formación de enlaces es entendible y es la sofisticación de los modelos iniciales de puntos de Lewis. La naturaleza cuántica del electrón hace que la formación de enlaces sea entendible físicamente y no se recurra a creencias como las que los químicos utilizaron antes de la aparición de la mecánica cuántica. Aún así, se obtuvo gran entendimiento a partir de la idea de puntos de Lewis.

Historia

Artículos principales: Historia de la química y Cronología de la química
Las primeras experiencias del hombre como químico se dieron con la utilización del fuego en la transformación de la materia, la obtención de hierro a partir del mineral y de vidrio a partir de arena son claros ejemplos. Poco a poco el hombre se dio cuenta de que otras sustancias también tienen este poder de transformación. Se dedicó un gran empeño en buscar una sustancia que transformara un metal en oro, lo que llevó a la creación de la alquimia. La acumulación de experiencias alquímicas jugó un papel vital en el futuro establecimiento de la química.
La química es una ciencia empírica, ya que estudia las cosas por medio del método científico, es decir, por medio de la observación, la cuantificación y, sobre todo, la experimentación. En su sentido más amplio, la química estudia las diversas sustancias que existen en nuestro planeta así como las reacciones que las transforman en otras sustancias. Por otra parte, la química estudia la estructura de las sustancias a su nivel molecular. Y por último, pero no menos importante, sus propiedades.

Subdisciplinas de la química

La química cubre un campo de estudios bastante amplio, por lo que en la práctica se estudia de cada tema de manera particular. Las seis principales y más estudiadas ramas de la química son:[cita requerida]
  • Química inorgánica: Síntesis y estudio de las propiedades eléctricas, magnéticas y ópticas de los compuestos formados por átomos que no sean de carbono (aunque con algunas excepciones). Trata especialmente los nuevos compuestos con metales de transición, los ácidos y las bases, entre otros compuestos.
  • Química orgánica: Síntesis y estudio de los compuestos que se basan en cadenas de carbono.
  • Bioquímica: estudia las reacciones químicas en los seres vivos, estudia el organismo y los seres vivos.
  • Química física: estudia los fundamentos y bases físicas de los sistemas y procesos químicos. En particular, son de interés para el químico físico los aspectos energéticos y dinámicos de tales sistemas y procesos. Entre sus áreas de estudio más importantes se incluyen la termodinámica química, la cinética química, la electroquímica, la mecánica estadística y la espectroscopía. Usualmente se la asocia también con la química cuántica y la química teórica.
  • Química industrial: Estudia los métodos de producción de reactivos químicos en cantidades elevadas, de la manera económicamente más beneficiosa. En la actualidad también intenta aunar sus intereses iniciales, con un bajo daño al medio ambiente.
  • Química analítica: estudia los métodos de detección (identificación) y cuantificación (determinación) de una sustancia en una muestra. Se subdivide en Cuantitativa y Cualitativa.
Además existen múltiples subdisciplinas, que por ser demasiado específicas, o multidisciplinares, se estudian individualmente:[cita requerida]

Los aportes de célebres autores

Hace aproximadamente cuatrocientos cincuenta y cinco años, sólo se conocían doce elementos. A medida que fueron descubriendo más elementos, los científicos se dieron cuenta de que todos guardaban un orden preciso. Cuando los colocaron en una tabla ordenados en filas y columnas, vieron que los elementos de una misma columna tenían propiedades similares. Pero también aparecían espacios vacíos en la tabla para los elementos aún desconocidos. Estos espacios huecos llevaron al científico ruso Dmitri Mendeléyev a pronosticar la existencia del germanio, de número atómico 32, así como su color, peso, densidad y punto de fusión. Su “predicción sobre otros elementos como - el galio y el escandio - también resultó muy atinada”, señala la obra Chemistry, libro de texto de química editado en 1995.

Campo de trabajo: el átomo

El origen de la teoría atómica se remonta a la escuela filosófica de los atomistas, en la Grecia antigua. Los fundamentos empíricos de la teoría atómica, de acuerdo con el método científico, se debe a un conjunto de trabajos hechos por Antoine Lavoisier, Louis Proust, Jeremias Benjamin Richter, John Dalton, Gay-Lussac y Amadeo Avogadro entre muchos otros, hacia principios del siglo XIX.
Los átomos son la fracción más pequeña de materia estudiados por la química, están constituidos por diferentes partículas, cargadas eléctricamente, los electrones, de carga negativa; los protones, de carga positiva; los neutrones, que, como su nombre indica, son neutros (sin carga); todos ellos aportan masa para contribuir al peso.

Conceptos fundamentales

Partículas

Los átomos son las partes más pequeñas de un elemento (como el carbono, el hierro o el oxígeno). Todos los átomos de un mismo elemento tienen la misma estructura electrónica (responsable esta de la gran mayoría de las características químicas), pudiendo diferir en la cantidad de neutrones (isótopos). Las moléculas son las partes más pequeñas de una sustancia (como el azúcar), y se componen de átomos enlazados entre sí. Si tienen carga eléctrica, tanto átomos como moléculas se llaman iones: cationes si son positivos, aniones si son negativos.
El mol se usa como contador de unidades, como la docena (12) o el millar (1000), y equivale a 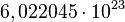6,022045\cdot10^{23}. Se dice que 12 gramos de carbono o un gramo de hidrógeno o 56 gramos de hierro contienen aproximadamente un mol de átomos (la masa molar de un elemento está basada en la masa de un mol de dicho elemento). Se dice entonces que el mol es una unidad de cambio. El mol tiene relación directa con el número de Avogadro. El número de Avogadro fue estimado para el átomo de carbono por el Químico y Físico italiano Carlo Amedeo Avogadro Conde de Quarequa e di Cerreto. Este valor, expuesto anteriormente, equivale al número de partículas presentes en 1 mol de dicha sustancia. Veamos:
1 mol de glucosa equivale a 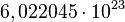6,022045\cdot10^{23} moléculas de glucosa
1 mol de Uranio equivale a 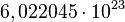6,022045\cdot10^{23} átomos de Uranio
Dentro de los átomos, podemos encontrar un núcleo atómico y uno o más electrones. Los electrones son muy importantes para las propiedades y las reacciones químicas. Dentro del núcleo se encuentran los neutrones y los protones. Los electrones se encuentran alrededor del núcleo. También se dice que es la unidad básica de la materia con características propias. Está formado por un núcleo donde se encuentran protones.

De los átomos a las moléculas

Los enlaces son las uniones entre átomos para formar moléculas. Siempre que existe una molécula es porque ésta es más estable que los átomos que la forman por separado. A la diferencia de energía entre estos dos estados se le denomina energía de enlace.
Generalmente, los átomos se combinan en proporciones fijas para dar moléculas. Por ejemplo, dos átomos de hidrógeno se combinan con uno de oxígeno para dar una molécula de agua. Esta proporción fija se conoce como estequiometría.

Orbitales

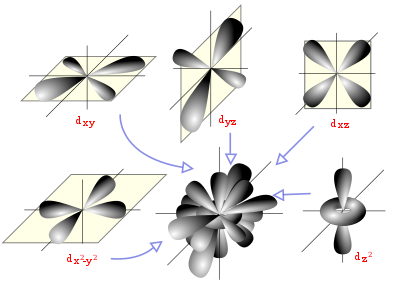
Diagrama espacial mostrando los orbitales atómicos hidrogenoides de momento angular del tipo d (l=2).
Artículos principales: Orbital atómico y orbital molecular
Para una descripción y comprensión detalladas de las reacciones químicas y de las propiedades físicas de las diferentes sustancias, es muy útil su descripción a través de orbitales, con ayuda de la química cuántica.
Un orbital atómico es una función matemática que describe la disposición de uno o dos electrones en un átomo. Un orbital molecular es análogo, pero para moléculas.
En la teoría del orbital molecular la formación del enlace covalente se debe a una combinación matemática de orbitales atómicos (funciones de onda) que forman orbitales moleculares, llamados así por que pertenecen a toda la molécula y no a un átomo individual. Así como un orbital atómico (sea híbrido o no) describe una región del espacio que rodea a un átomo donde es probable que se encuentre un electrón, un orbital molecular describe una región del espacio en una molécula donde es más factible que se hallen los electrones.
Al igual que un orbital atómico, un orbital molecular tiene un tamaño, una forma y una energía específicos. Por ejemplo, en la molécula de hidrógeno molecular se combinan dos orbitales atómicos uno s ocupados cada uno por un electrón. Hay dos formas en que puede presentarse la combinación de orbitales: aditiva y subtractiva. La combinación aditiva produce la formación de un orbital molecular que tiene menor energía y que tiene, aproximadamente, forma ovalada, mientras que la combinación subtractiva conduce a la formación de un orbital molecular con mayor energía y que genera un nodo entre los núcleos.

De los orbitales a las sustancias

Los orbitales son funciones matemáticas para describir procesos físicos: un orbital solo existe en el sentido matemático, como pueden existir una suma, una parábola o una raíz cuadrada. Los átomos y las moléculas son también idealizaciones y simplificaciones: un átomo sólo existe en vacío, una molécula sólo existe en vacío, y, en sentido estricto, una molécula sólo se descompone en átomos si se rompen todos sus enlaces.
En el "mundo real" sólo existen los materiales y las sustancias. Si se confunden los objetos reales con los modelos teóricos que se usan para describirlos, es fácil caer en falacias lógicas.

Disoluciones

Artículo principal: Disolución
En agua, y en otros disolventes (como la acetona o el alcohol), es posible disolver sustancias, de forma que quedan disgregadas en las moléculas o iones que las componen (las disoluciones son transparentes). Cuando se supera cierto límite, llamado solubilidad, la sustancia ya no se disuelve, y queda, bien como precipitado en el fondo del recipiente, bien como suspensión, flotando en pequeñas partículas (las suspensiones son opacas o traslúcidas).
Se denomina concentración a la medida de la cantidad de soluto por unidad de cantidad de disolvente.

Medida de la concentración

Artículo principal: Concentración
La concentración de una disolución se puede expresar de diferentes formas, en función de la unidad empleada para determinar las cantidades de soluto y disolvente. Las más usuales son:

Acidez

Artículo principal: pH
El pH es una escala logarítmica para describir la acidez de una disolución acuosa. Los ácidos, como el zumo de limón y el vinagre, tienen un pH bajo (inferior a 7). Las bases, como la sosa o el bicarbonato de sodio, tienen un pH alto (superior a 7).
El pH se calcula mediante la siguiente ecuación:
pH= -\log a_{H^+} \approx -\log [H^+]\,
donde a_{H^+}\, es la actividad de iones hidrógeno en la solución, la que en soluciones diluidas es numéricamente igual a la molaridad de iones Hidrógeno [H^+]\, que cede el ácido a la solución.
  • una solución neutral (agua ultra pura) tiene un pH de 7, lo que implica una concentración de iones hidrógeno de 10-7 M
  • una solución ácida (por ejemplo, de ácido sulfúrico)tiene un pH < 7, es decir que la concentración de iones hidrógeno es mayor que 10-7 M
  • una solución básica (por ejemplo, de hidróxido de potasio) tiene un pH > 7, o sea que la concentración de iones hidrógeno es menor que 10-7 M

Formulación y nomenclatura

La IUPAC, un organismo internacional, mantiene unas reglas para la formulación y nomenclatura química. De esta forma, es posible referirse a los compuestos químicos de forma sistemática y sin equívocos.
Mediante el uso de fórmulas químicas es posible también expresar de forma sistemática las reacciones químicas, en forma de ecuación química. Por ejemplo:
MgSO_{4} + Ca(OH)_{2} \rightleftharpoons CaSO_{4} + Mg(OH)_{2}
Publicado por en No hay comentarios:

los 7 problemas del milenio

Clases de complejidad P y NP


Diagrama de clases de complejidad para el caso en que P ≠ NP. La existencia de problemas fuera tanto de P como de NP-completos en este caso fue determinada por Ladner.[1]
La relación entre las clases de complejidad P y NP es una pregunta que aún no ha podido ser respondida por la teoría de la complejidad computacional. En esencia, la pregunta ¿es P = NP ? significa: si es posible "verificar" rápidamente soluciones positivas a un problema del tipo SI/NO (donde "rápidamente" significa "en tiempo polinómico"), ¿es que entonces también se pueden "obtener" las respuestas rápidamente?
Los recursos comúnmente estudiados en complejidad computacional son:
– El tiempo: mediante una aproximación al número de pasos de ejecución que un algoritmo emplea para resolver un problema.
– El espacio: mediante una aproximación a la cantidad de memoria utilizada para resolver el problema.
Los problemas se clasifican en conjuntos o clases de complejidad (L, NL, P, PCompleto, NP, NP-Completo, NP Duro...).Nosotros nos vamos a centrar en las clases P y NP.
Se lo considera el problema más importante en este campo--el Clay Mathematics Institute ha ofrecido un premio de $1 millón de dólares norteamericanos para quién desarrolle la primera demostración correcta.

Ejemplo

Consideremos, por ejemplo, el Problema de la suma de subconjuntos, que es un ejemplo de un problema fácil de verificar, pero cuya respuesta se cree (pero no ha sido demostrado) es difícil de calcular/hallar. Dado un conjunto de números enteros, ¿existe un subconjunto no vacío de ellos donde la suma de sus elementos es igual a 0? por ejemplo, ¿existe un subconjunto del conjunto {−2, −3, 15, 14, 7, −10} tal que la suma de sus elementos sea 0? La respuesta es SI, si bien puede llevar algún tiempo encontrar un subconjunto que satisface el requerimiento, según cual sea el tamaño del conjunto y subconjunto. Por otra parte, si alguien afirma que la respuesta es: «sí, porque la suma de {−2, −3, −10, 15} es igual a cero», entonces lo podemos comprobar en forma muy rápida y mediante unas pocas cuentas. Verificar que la suma del subconjunto es cero es un proceso mucho más rápido que encontrar el subconjunto. La información necesaria para verificar un resultado positivo/afirmativo es llamada un certificado. Por lo que podemos concluir que dado los certificados apropiados, es posible verificar rápidamente las respuestas afirmativas de nuestro problema (en tiempo polinomial) y es ésta la razón por la que el problema se encuentra en NP. Una respuesta a la pregunta P = NP sería determinar si en problemas del tipo SUMA-SUBCONJUNTO es tan fácil hallar la solución como verificarla. Si se encuentra que P no es igual a NP, ello significa que algunos problemas NP serían significativamente más difíciles de hallar su solución que verificar la misma. La respuesta sería aplicable a todo este tipo de problemas, no solo al ejemplo específico de SUMA-SUBCONJUNTO.
La restricción a problemas de tipo SI/NO realmente no es importante; aún si se permiten respuestas más complicadas, el problema resultante resulta equivalente (o sea si FP = FNP).

Contexto del problema

La relación entre las clases de complejidad P y NP es estudiada por la teoría de la complejidad computacional, la parte de la teoría de la computación que trata de los recursos requeridos durante el cálculo para resolver un problema dado. Los recursos más usuales son tiempo (¿cuántos pasos son necesarios para resolver un problema?) y espacio (¿cuánta memoria es necesaria para resolver un problema?).
En este tipo de análisis, se requiere un modelo de la computadora para la que desea estudiar el requerimiento en términos de tiempo. Típicamente, dichos modelos suponen que la computadora es determinística (dado el estado actual de la computadora y las variables de entrada, existe una única acción posible que la computadora puede tomar) y secuencial (realiza las acciones una después de la otra). Estas suposiciones son adecuadas para representar el comportamiento de todas las computadoras existentes, aún incluye a las máquinas con computación en paralelo.
En esta teoría, la clase P consiste de todos aquellos problemas de decisión que pueden ser resueltos en una máquina determinística secuencial en un período de tiempo polinomial en proporción a los datos de entrada. En la teoría de complejidad computacional, la clase P es una de las más importantes; la clase NP consiste de todos aquellos problemas de decisión cuyas soluciones positivas/afirmativas pueden ser verificadas en tiempo polinómico a partir de ser alimentadas con la información apropiada, o en forma equivalente, cuya solución puede ser hallada en tiempo polinómico en una máquina no-determinística. Por lo tanto, la principal pregunta aún sin respuesta en la teoría de la computación está referida a la relación entre estas dos clases:
¿Es P igual a NP?

En una encuesta realizada en el 2002 entre 100 investigadores, 61 creían que la respuesta era NO, 9 creían que la respuesta era SI, 22 no estaban seguros, y 8 creían que la pregunta podía ser independiente de los axiomas actualmente aceptados, y por lo tanto imposible de demostrar por el SI o por el NO.[2]

 Definiciones formales

Más precisamente, un problema de decisión es un problema que especifica una cadena de caracteres de datos de entrada y requiere como solución una respuesta por el SI o por el NO. Si existe un algoritmo (por ejemplo una máquina de Turing, o un programa en lenguajes Lisp o Pascal con memoria irrestricta) que es capaz de entregar la respuesta correcta para toda cadena de datos de longitud n en a lo sumo pasos, donde k y c son constantes independientes del conjunto de datos, entonces se dice que el problema puede ser resuelto en tiempo polinómico y lo clasificamos como perteneciente a la clase P. En forma intuitiva, consideramos que los problemas contenidos en P son aquellos que pueden ser resueltos en forma razonablemente rápida.
P suele ser la clase de problemas computacionales que son “eficientemente resolubles” o “tratables”, aunque haya clases potencialmente más grandes que también se consideran tratables, como RP Y BPP. Aunque también existen problemas en P que no son tratables en términos prácticos; por ejemplo, unos requieren al menos n1000000 operaciones.
En forma intuitiva, se puede pensar que NP es un problema de decisión que es difícil de resolver si no se posee ningún otro dato o información adicional. Sin embargo, si se recibe la información adicional llamada un certificado, entonces el problema puede ser resuelto fácilmente. Por ejemplo, si se nos da el número 323 y se nos pregunta si 323 es un número factorizable, sin darnos ningún dato o información adicional, deberíamos analizar todos los números enteros positivos mayores que 2 pero menores que 323 para estudiar si alguno de ellos divide exactamente al 323. Sin embargo, si se nos da el número 17, podemos dividir 323 por 17 y rápidamente verificar que 323 es factorizable. El número 17 es llamado un certificado. El proceso de división para verificar que 323 es factorizable es en esencia una máquina Turing y en este caso es denominado el verificador para 323. Técnicamente se dice que el problema es fácil si se puede resolver en tiempo polinómico y que es difícil si se resuelve en tiempo exponencial. Formalmente, se define NP como un conjunto de lenguajes que satisfacen ciertas condiciones.
Sea L un lenguaje definido sobre un alfabeto finito, Σ.
Si existe una relación binaria y un entero positivo k tal que para todo , se satisfacen las siguientes condiciones:
(i) tal que y O .
(ii) El lenguaje LR= en es decible.

Entonces, la máquina de Turing que decide LR (que la llamaremos V) es llamada el Verificador para L y y es llamado el Certificado de membresía de x en L.
Finalmente, L se encuentra en NP "si y solo si" V corre en tiempo polinómico.
Ejemplo.
Sea COMPOSITE =
R =
Claramente, la pregunta de si un dado x es factorizable es equivalente a la pregunta sobre si x es un miembro de COMPOSITE. De hecho, se puede demostrar fácilmente que si se verifica que COMPOSITE satisface la condición indicada previamente.
(Nota. Recientemente se demostró que COMPOSITE estaba dentro de P[3] )

 La clase P

P es conocido por contener muchos problemas naturales, incluyendo las versiones de decisión de programa lineal, cálculo del máximo común divisor, y encontrar una correspondencia máxima.
Problemas notables en P
Algunos problemas naturales son completos para P, incluyendo la conectividad (o la accesibilidad) en grafos no dirigidos.
Una generalización de P es NP, que es la clase de lenguajes decidibles en tiempo polinómico sobre una máquina de Turing no determinista. De forma trivial, tenemos que P es un subconjunto de NP. Aunque no está demostrado, la mayor parte de los expertos creen que esto es un subconjunto estricto.
Aquí, EXPTIME es la clase de problemas resolubles en tiempo exponencial. De todas las clases mostradas arriba, sólo se conocen dos contenciones estrictas:
  • P estrictamente está contenido en EXPTIME.
  • L estrictamente está contenida en PSPACE.

Los problemas más difíciles en P son los problemas P-completos
Otra generalización de P es el Tiempo polinómico No uniforme (P/Poly)[1]. Si un problema está en P/poly, entonces puede solucionarse en un tiempo polinomial determinado el cual, dado una cadena, este solo depende de la longitud de la entrada. A diferencia de NP, no se comprueban las cadenas defectuosas que entran en la máquina de Turing, puesto que no es un verificador.
P/poly es una clase grande que contiene casi todos los algoritmos prácticos, incluyendo todo el BPP. Si esta contiene a NP, la jerarquía polinomial se colapsa con el segundo nivel. Por otra parte, esta también contiene algunos algoritmos poco prácticos, incluyendo algunos problemas no decidibles.
Propiedades
Los algoritmos de tiempo polinómico son cerrados respecto a la composición. Intuitivamente, esto quiere decir que si uno escribe una función con un determinado tiempo polinómico y consideramos que las llamadas a esa misma función son constantes y, de tiempo polinómico, entonces el algoritmo completo es de tiempo polinómico. Esto es uno de los motivos principales por los que P se considera una máquina independiente; algunos rasgos de esta máquina, como el acceso aleatorio, es que puede calcular en tiempo polinómico el tiempo polinómico del algoritmo principal reduciéndolo a una máquina más básica.
Las pruebas existenciales de algoritmos de tiempo polinómico
Se conoce que algunos problemas son resolubles en tiempo polinómico, pero no se conoce ningún algoritmo concreto para solucionarlos. Por ejemplo, el teorema Robertson-Seymour garantiza que hay una lista finita de los menores permitidos que compone (por ejemplo) el conjunto de los grafos que pueden ser integrados sobre un toroide; además, Robertson y Seymour demostraron que hay una complejidad O (n3) en el algoritmo para determinar si un grafo tiene un grafo incluido. Esto nos da una prueba no constructiva de que hay un algoritmo de tiempo polinómico para determinar si dado un grafo puede ser integrado sobre un toroide, a pesar de no conocerse ningún algoritmo concreto para este problema.
Ejemplos
Camino Mínimo: encontrar el camino mínimo desde un vértice origen al resto de los vértices.
Ciclo Euleriano: Encontrar un ciclo que pase por cada arco de un grafo una única vez.

 La clase NP

La clase NP está compuesta por los problemas que tienen un certificado sucinto (también llamado testigo polinómico) para todas las instancias cuya respuesta es un SÍ. La única forma de que tengan un tiempo polinomial es realizando una etapa aleatoria, incluyendo el azar de alguna manera para elegir una posible solución, y entonces en etapas posteriores comprueba si esa solución es correcta.
En otras palabras, dada una solución para una cierta instancia, es posible comprobar que es válida en TIME (n^k). En el caso de SAT (Problema de satisfacibilidad booleana), dado una asignación de valores de verdad, se puede comprobar fácilmente si la fórmula es cierta o no. Una nMT puede "adivinar" la solución en O (n) y verificarla en tiempo polinómico.
Completitud de NP
Para analizar la pregunta P = NP, resulta muy útil el concepto de completitud NP. De manera informal, los problemas de completitud NP son los problemas más "difíciles" en NP en el sentido de que ellos son los que son más probable no se encuentren en P. Problemas NP-difíciles son aquellos para los cuales cualquier problema en NP puede ser reducido en tiempo polinómico. Los problemas de completitud NP son aquellos problemas NP-difícil que se encuentran en NP. Por ejemplo, la versión de problema de decisión del problema del vendedor viajero es completamente NP. Así ningún caso de ningún problema en NP puede ser transformado mecánicamente en una parte del problema del vendedor viajero, en tiempo polinómico. Por lo tanto, si el problema del vendedor viajero estuviera contenido en P, entonces P = NP. El problema del vendedor viajero es uno de muchos problemas NP-completos. Si cualquier problema NP-completo se encuentra contenido en P, entonces se verificaría que P = NP. Desafortunadamente, se ha demostrado que muchos problemas importantes son NP-completos y no se conoce la existencia de ningún algoritmo rápido para ellos.
La definición anterior de NP permite considerar de manera natural una clase de problemas complementarias. La co-NP está compuesta por los problemas que tienen un contraejemplo sucinto para todas las instancias cuya respuesta es NO.
Problema Clique
Denominamos Clique al siguiente problema:
Dado un grafo G y un entero k, ¿es posible encontrar un subgrafo de G completo de tamaño k?
• Claramente Clique pertenece a NP.
• Ahora deberemos hacer una reducción de SAT a NP.
• Supongamos que tenemos una fórmula en CNF:
C1 v C2 v . . . v Ck con n variables proposicionales.
Formaremos un grafo G con un nodo por cada literal que aparece en cada cláusula. Cada nodo está etiquetado con el literal que le dio origen. Agregaremos un arco entre un nodo etiquetado con l y un nodo etiquetado con l0 si y solo si:
– l y l0 están en cláusulas distintas.
– l no es el literal complementario de l.
Supongamos la siguiente fórmula: (x1 v x2 v ¬x3) ^ (¬x1 v ¬x3) ^ (x3 v x2). El grafo resultante queda como:

Ahora deberemos demostrar que G tiene un subgrafo completo de tamaño k si es satisfactible. Como todos los miembros del subgrafo pertenecen a cláusulas distintas, cualquier valuación que hace verdadero a todo literal en el subgrafo hace verdadera a la fórmula (recordemos que dos literales complementarios no pueden estar en un subgrafo completo). Si la fórmula es satisfecha, debe existir una valuación que haga verdaderos a al menos un literal en cada cláusula. Sean l1 pertenece a C1, l2 pertenece a C2, . . . , lk pertenece Ck estos literales. Notemos que no es posible que existan dos literales complementarios li y lj. Necesariamente, entonces, podemos construir arcos entre cada par de nodos en donde aparecen dichos literales siguiendo las reglas de construcción del grafo.

Ejemplos
Camino Máximo: Dados dos vértices de un grafo encontrar el camino (simple) máximo.
Ciclo Hamiltoniano: Ciclo simple que contiene cada vértice del grafo.

 NP-Completo

Para abordar la pregunta de si P=NP, el concepto de la completitud de NP es muy útil. Informalmente, los problemas de NP-completos son los problemas más difíciles de NP, en el sentido de que son los más probables de no encontrarse en P. Los problemas de NP-completos son esos problemas NP-duros que están contenidos en NP, donde los problemas NP-duros son estos que cualquier problema en NP puede ser reducido a complejidad polinomial. Por ejemplo, la decisión del Problema del viajante de comercio es NP-completo, así que cualquier caso de cualquier problema en NP puede ser transformado mecánicamente en un caso del Problema del viajante de comercio, de complejidad polinomial. El Problema del viajante de comercio es de los muchos problemas NP-completos existentes. Si cualquier problema NP-completo estuviera en P, entonces indicaría que P=NP. Desafortunadamente, se sabe que muchos problemas importantes son NP-completos y a fecha de 2008, no se conoce ningún algoritmo rápido para ninguno de ellos. Basándonos solo en esta idea, no es obvio que exista un problema NP-completo. Un problema NP-completo trivial e ideado, se puede formular como: Dada una descripción de una máquina de Turing M que se detiene en tiempo polinómico, ¿existe una entrada de tamaño polinómico que M acepte? Es NP porque, dada una entrada, es simple comprobar si M acepta o no la entrada simulando M, es NP-duros porque el verificador para cualquier caso particular de un problema en NP puede ser codificado como una maquina M de tiempo polinomial que toma la solución para ser verificada como entrada. Entonces la pregunta de si el caso es o no un caso, esta determinado por la existencia de una entrada valida. El primer problema natural que se demostró ser NP-completo fue el Problema booleano de satisfacibilidad. Este resultado es conocido como el teorema de Cook-Levin; su prueba de que la satisfacibilidad es NP-completo contiene los detalles técnicos sobre máquinas de Turing y como se relacionan con la definición de NP. Sin embargo, después se demostró que el problema era NP-completo, la prueba por reducción, proporcionó una manera más simple de demostrar que muchos otros problemas están en esta clase. Así, una clase extensa de problemas aparentemente sin relación es reducible a otra, y son en este sentido el mismo problema.


Conjetura de Hodge

De Wikipedia, la enciclopedia libre
Saltar a: navegación, búsqueda
La conjetura de Hodge es un importante problema de geometría algebraica todavía no resuelto en el que se relacionan la topología algebraica de una variedad algebraica compleja no singular y las subvariedades de esa variedad. En concreto, la conjetura dice que ciertos grupos de cohomología de De Rham son algebraicos, esto es, son sumas de dualidades de Poincaré de clases homólogas de subvariedades.
La conjetura de Hodge es uno de los Problemas del milenio del Clay Mathematics Institute, por lo que hay un premio de US$1,000,000 por demostrarla.

 Motivación

Sea X una variedad compleja conexa de dimensión compleja n. Luego X es una variedad diferenciable orientable de dimensión 2n, por lo que sus grupos de cohomología residen en grados cero a través de 2n. Asúmase que X es una variedad de Kähler, por lo que hay una decomposición en su cohomología con coeficientes complejos:
donde Hp,q(X) es el subgrupo de grupos de cohomología que están representados por formas armónicas de tipo (p, q). Esto es, estas son los grupos de cohomología representados por formas diferenciales que, en una determinada opción de coordenadas locales , puede ser escritas como tiempos de funciones armónicas . (Véase Teoría de Hodge para más detalles). Tomar productos exteriores de estos representantes armónicos se corresponde con el cup product en cohomología, por lo que cup product es compatible con la decomposición de Hodge:
Dado que X es una variedad compleja, X tiene una clase fundamental.
Sea Z una subvariedad compleja de X de dimensión k, y sea i : Z → X la función de inclusión. Elíjase una forma diferenciada α del tipo (p, q). Podemos integrar α sobre Z:
Para evaluar esta integral, elíjase un punto de Z y llámesele 0. Alrededor de 0, podemos elegir coordinadas locales en X tal que Z sea . If p > k, entonces α debe contener algún dzi donde zi tienda a a cero en Z. Lo mismo es cierto si q > k. Consecuentemente, esta integral es cero si (p, q) ≠ (k, k).
De forma más abstracta, la integral puede ser escrita como el cap product del grupo de cohomología de Z y del grupo de cohomología representado por α. Según la dualidad de Poincaré, el grupo de homología de Z es doble del grupo de cohomología que llamaremos [Z], y el cap product puede ser calculado tomando el cup product de [Z] y α y capping con la clase fundamental de X. Dado que [Z] es un grupo de cohomología, tiene decomposición de Hodge. Según el cálculo anterior, si nosotros cup este grupo con otro tipo de grupo (p, q) ≠ (k, k), entonces tendremos cero. Dado que , se concluye que [Z] debe quedar en . En pocas palabras, la conjetura de Hodge dice:
¿Qué grupos de cohomología en Hk,k(X) derivan de subvariedades complejas Z?




Hipótesis de Riemann

De Wikipedia, la enciclopedia libre
(Redirigido desde Conjetura de Riemann)
Saltar a: navegación, búsqueda
Parte real (rojo) y parte imaginaria (azul) de la línea crítica Re(s) = 1/2 de la función zeta de Riemann. Pueden verse los primeros ceros no triviales en Im(s) = ±14,135, ±21,022 y ±25,011.
Un gráfico polar de zeta, esto es, Re(zeta) vs. Im(zeta), a lo largo de la línea crítica s=it+1/2, con t con valores desde 0 a 34.
En matemática pura, la hipótesis de Riemann, formulada por primera vez por Bernhard Riemann en 1859, es una conjetura sobre la distribución de los ceros de la función zeta de Riemann ζ(s).[1]
La hipótesis de Riemann, por su relación con la distribución de los números primos en el conjunto de los naturales, es uno de los problemas abiertos más importantes en la matemática contemporánea.
Se ha ofrecido un premio de un millón de dólares por el Instituto Clay de Matemáticas para la primera persona que desarrolle una demostración correcta de la conjetura.[2] La mayoría de la comunidad matemática piensa que la conjetura es cierta, aunque otros grandes matemáticos como J. E. Littlewood y Atle Selberg se mostraron escépticos, si bien el escepticismo de Selberg fue disminuyendo desde sus días de juventud. En un artículo en 1989 sugirió que un análogo debe ser cierto para una clase mucho más amplia de funciones (la

Definición

La función zeta de Riemann ζ(s) está definida de la siguiente manera:
Para todos los números complejos s ≠ 1, se puede prolongar analíticamente mediante la ecuación funcional:
Ésta posee ciertos valores, llamados ceros "triviales" para los cuales la función zeta se anula. De la ecuación se puede ver que s = −2, s = −4, s = −6, ... son ceros triviales. Existen otros valores complejos s comprendidos entre 0 < Re(s) < 1, para los cuales la función zeta también se anula, llamados ceros "no triviales". La conjetura de Riemann hace referencia a éstos ceros no triviales afirmando:
La parte real de todo cero no trivial de la función zeta de Riemann es 1/2

Por lo tanto los ceros no triviales deberían encontrarse en la línea crítica s = 1/2 + i t donde t es un número real e i es la unidad imaginaria. La función zeta de Riemann, a lo largo de la línea crítica ha sido estudiada en términos de la función Z, cuyos ceros corresponden a los ceros de la función zeta sobre la línea crítica.

 Historia

Riemann mencionó la conjetura, que sería llamada la hipótesis de Riemann, en su artículo de 1859 Sobre los números primos menores que una magnitud dada, al desarrollar una fórmula explícita para calcular la cantidad de primos menores que x. Puesto que no era esencial para el propósito central de su artículo, no intentó dar una demostración de la misma. Riemann sabía que los ceros no triviales de la función zeta están distribuidos en torno a la recta s = 1/2 + i t, y sabía también que todos los ceros no triviales debían estar en el rango 0 ≤ Re(s) ≤ 1.[3]
En 1896, Hadamard y de la Vallée-Poussin probaron independientemente, que ningún cero podía estar sobre la recta Re(s) = 1. Junto con las otras propiedades de los ceros no triviales demostradas por Riemann, esto mostró que todos los ceros no triviales deben estar en el interior de la banda crítica 0 < Re(s) < 1. Este fue un paso fundamental para las primeras demostraciones del teorema de los números primos.
En 1900, Hilbert incluyó la hipótesis de Riemann en su famosa lista de los 23 problemas no resueltos — es parte del problema 8 en la lista de Hilbert junto con la conjetura de Goldbach. Cuando se le preguntó qué haría si se despertara habiendo dormido quinientos años, remarcablemente Hilbert contestó que su primera pregunta sería si la hipótesis de Riemann había sido probada. La hipótesis de Riemann es el único problema de los que propuso Hilbert que está en el premio del milenio del Instituto Clay de Matemáticas.
En 1914, Hardy demostró que existe un número infinito de ceros sobre la recta crítica Re(s) = 1/2. Sin embargo todavía era posible que un número infinito (y posiblemente la mayoría) de los ceros no triviales se encontraran en algún otro lugar sobre la banda crítica. En trabajos posteriores de Hardy y Littlewood en 1921 y de Selberg en 1942 se dieron estimaciones para la densidad promedio de los ceros sobre la línea crítica.
Trabajos recientes se han concentrado en el cálculo explícito de la localización de grandes cantidades de ceros (con la esperanza de hallar algún contraejemplo) y en el establecimientos de cotas superiores en la proporción de ceros que puedan estar lejos de la línea crítica (con la esperanza de reducirlas a cero).

 La hipótesis de Riemann y los números primos

La formulación tradicional de la hipótesis de Riemann oscurece un poco la importancia real de la conjetura. La función zeta de Riemann tiene una profunda conexión con los números primos y Hege von Koch demostró en 1901 que la hipótesis de Riemann es equivalente al considerable refinamiento del teorema de los números primos: Existe una constante C > 0 tal que
para todo x suficientemente grande, donde π(x) es la función contadora de primos y ln(x) es el logaritmo natural de x. Lowell Schoenfeld mostró que se puede tomar C = 1/(8 π) para todo x ≥ 2657.
Los ceros de la función zeta y los números primos satisfacen ciertas propiedades de dualidad, conocidas como fórmulas explícitas, que muestran, usando análisis de Fourier, que los ceros de la función zeta de Riemann pueden interpretarse como frecuencias armónicas en la distribución de los números primos.
Más aún, si la conjetura de Hilbert-Polya es cierta, entonces cualquier operador que nos dé las partes imaginarias de los ceros como sus valores propios debe satisfacer:
donde Tr es la traza del operador (suma de sus valores propios) , β es un número imaginario y ψ(x) es la Función de Chebyshov que nos suma el log(x) sobre los primos y sus potencias enteras, dicha fórmula es una conclusión de la 'fórmula explicita' de V. Mangoldt.[4] Varios operadores propuestos por C. Perelman, J. Macheca y J. Garcia, parecen corroborar los resultados de la conjetura de Hilbert sobre el operador, reproduciendo la parte imaginaria de los ceros.

 Cálculo numérico

Valor absoluto de la ζ-function.
  • En el año 2004 Xavier Gourdon verificó la conjetura de Riemann numéricamente a lo largo de los primeros diez trillones de ceros no triviales de la función. Sin embargo esto no es estrictamente una demostración, numéricamente es más interesante encontrar un contraejemplo, es decir un valor de cero que no cumpla con que su parte real es 1/2, pues esto echaría por los suelos la validez de la conjetura.
  • Hasta el 2005, el intento más serio para explorar los ceros de la función-ζ, es el ZetaGrid, un proyecto de computación distribuida con la capacidad de verificar billones de ceros por día. El proyecto acabó en diciembre de 2005, y ninguno de los ceros pudo ser identificado como contraejemplo de la hipótesis de Riemann.

Véase también

Función diferenciable

De Wikipedia, la enciclopedia libre
Saltar a: navegación, búsqueda
El concepto de función diferenciable es una generalización para el cálculo en varias variables del concepto más simple de función derivable. En esencia una función diferenciable admite derivadas en cualquier dirección y puede aproximarse al menos hasta primer orden por una aplicación afín.
La formulación rigurosa de esta idea intuitiva sin embargo es algo más complicada y requiere de conocimientos de álgebra lineal. Debe notarse que aunque una función de varias variables admita derivadas parciales según cada una de sus variables no necesariamente eso implica que sea una función diferenciable.

Definición

Una función de varias variables se dirá diferenciable en si , siendo Ω un conjunto abierto en , si existe una transformación lineal que cumpla:
Donde θ(h) cumple que:
o sea θ(h) tiende a cero "más rápido" que función lineal, cuando h tiende a 0. Necesariamente la transformación lineal es la única cosa que se ve más claramente si adoptamos como definición de función derivable aquella para la cual se cumple que exista una aplicación lineal tal que:

 Visualización Geométrica

Para fijar ideas, usando una función cuyo gráfico sería una "sábana". La función es diferenciable si la "sábana" no está "quebrada" en los puntos donde es diferenciable, o sea la función es "suave" en todos los puntos de su dominio, existiendo la matriz jacobiana o derivada en esos puntos.

 Ejemplos

 De función diferenciable

La función f(x,y) es diferenciable, si x ,y son diferentes de 0 puesto que existen las derivadas parciales en un entorno de cualquier punto y son continuas en él:

 De función derivable no-diferenciable

En cambio la función g(x,y) es continua, admite derivadas según las variables x e y, e incluso derivadas direccionales, sin embargo no es diferenciable en (0,0):

 De función no-continua y no-diferenciable

La función no es diferenciable en (0,0) puesto que no es continua en ese punto a pesar de que existen derivadas parciales de cualquier orden en el punto (0,0):

Ecuaciones de Navier-Stokes

De Wikipedia, la enciclopedia libre
Saltar a: navegación, búsqueda
Las ecuaciones de Navier-Stokes reciben su nombre de Claude-Louis Navier y George Gabriel Stokes. Se trata de un conjunto de ecuaciones en derivadas parciales no lineales que describen el movimiento de un fluido. Estas ecuaciones gobiernan la atmósfera terrestre, las corrientes oceánicas y el flujo alrededor de vehículos o proyectiles y, en general, cualquier fenómeno en el que se involucren fluidos newtonianos.
Estas ecuaciones se obtienen aplicando los principios de conservación de la mecánica y la termodinámica a un volumen fluido. Haciendo esto se obtiene la llamada formulación integral de las ecuaciones. Para llegar a su formulación diferencial se manipulan aplicando ciertas consideraciones, principalmente aquella en la que los esfuerzos tangenciales guardan una relación lineal con el gradiente de velocidad (ley de viscosidad de Newton), obteniendo de esta manera la formulación diferencial que generalmente es más útil para la resolución de los problemas que se plantean en la mecánica de fluidos.
Como ya se ha dicho, las ecuaciones de Navier-Stokes son un conjunto de ecuaciones en derivadas parciales no lineales. No se dispone de una solución general para este conjunto de ecuaciones, y salvo ciertos tipos de flujo y situaciones muy concretas no es posible hallar una solución analítica; por lo que en muchas ocasiones hemos de recurrir al análisis numérico para determinar una solución aproximada. A la rama de la mecánica de fluidos que se ocupa de la obtención de estas soluciones mediante el ordenador se la denomina dinámica de fluidos computacional (CFD, de su acrónimo anglosajón Computational Fluid Dynamics).

Conceptos previos

 Derivada sustancial o material

Artículo principal: Derivada sustancial
Debido a que generalmente adoptamos la descripción euleriana la derivada ordinaria ya no representa toda la variación por unidad de tiempo de una determinada propiedad del fluido ϕ siguiendo a la partícula fluida. Esto se debe al movimiento del fluido. Para reflejar esta variación usaremos la derivada sustancial (o derivada siguiendo a la partícula fluida). La derivada sustancial o derivada material se define como el operador:
Donde es la velocidad del fluido. El primer término representa la variación de la propiedad en un punto fijo del espacio y por ello se la denomina derivada local, mientras que el segundo representa la variación de la propiedad asociado al cambio de posición de la partícula fluida, y se la denomina derivada convectiva. Este es el procedimiento que sigue José de Echegaray para demostrar la derivada material. Véase una demostración de cómo llegar a una derivada material. Tomando las coordenadas de Euler como:
.
Calcularemos la aceleración para estas coordenadas:
Desarrollamos cada derivada total de cada componente, así podremos seguir un desarrollo fácil de recordar:
Si se suma término a término y se saca factor común, puede obtenerse:
Vemos que la parte de las derivadas parciales espaciales se pueden escribir como:
Si ahora sustituimos velocidad por obtenemos formalmente la expresión de la derivada material:

 Teorema del transporte de Reynolds

Artículo principal: Teorema del transporte de Reynolds
Si la derivada sustancial permite calcular la variación de una propiedad del fluido siguiendo a una partícula fluida, el teorema del transporte de Reynolds permitirá calcular la variación de una magnitud fluida extensiva ligada a un volumen fluido. En su forma general el teorema del transporte de Reynolds se expresa como:
donde ϕ es una propiedad extensiva definida por unidad de volumen, Vf es un volumen fluido, Vc es un volumen de control que coincide con Vf en el instante t, Sc la superficie de control ligada a dicho volumen, la velocidad del fluido y la velocidad de la superficie de control.
Expresado en términos coloquiales puede decirse que el teorema del transporte de Reynolds viene a decir que la variación de una propiedad extensiva en un volumen fluido, es igual a la variación de dicha propiedad en el interior de ese volumen más la cantidad de dicha propiedad que atraviesa la superficie del volumen.

 Teorema de la divergencia

Artículo principal: teorema de la divergencia
El teorema de la divergencia (o teorema de Gauss), nos permite transformar integrales de superficie en integrales de volumen ( y viceversa). En el caso particular de tres dimensiones podemos expresarlo como:

 Las ecuaciones de Navier-Stokes

Esta expresión representa el principio de conservación del momento lineal aplicada a un fluido general:
.
La ley de conservación de la masa se escribe:
En estas ecuaciones ρ representa la densidad, ui (i = 1,2,3) las componentes cartesianas de la velocidad, Fi las fuerzas aplicadas sobre el cuerpo, como la gravedad, P la presión del fluido, y μ la viscosidad dinámica.
donde Δ = eii es la divergencia del fluido y δij la delta de Kronecker. D / Dt es la derivada total o derivada material temporal siguiendo el fluido:
La no-linealidad de las ecuaciones se debe precisamente al término relacionado con la derivada total. Cuando μ es uniforme sobre todo el fluido las ecuaciones de fluido se simplifican de la manera siguiente:
O en forma vectorial:

 Fluidos no viscosos

Para fluidos de viscosidad nula, es decir cuando μ = 0, las ecuaciones resultantes se denominan ecuaciones de Euler que se utilizan en el estudio de fluidos compresibles y en ondas de choque. Si además ρ puede ser considerada constante (como en un líquido):
y la ecuación de continuidad adquiere la forma siguiente:

 Otras consideraciones



Conjetura de Birch y Swinnerton-Dyer

De Wikipedia, la enciclopedia libre
(Redirigido desde La conjetura de Birch y Swinnerton-Dyer)
Saltar a: navegación, búsqueda
La conjetura de Birch y Swinerton-Dyer fue enunciada en 1965 y establece una condición para que una curva algebraica plana, f(x, y) = 0, definida sobre los racionales —esto es, con los argumentos x, y∈ℚ—, tenga infinitos puntos racionales —esto es, (x, y) solución de f(x, y) = 0, con x, y∈ℚ—, como por ejemplo la circunferencia.
En 1970, Yuri Matiyasévich demostró que no existe algoritmo posible para determinar si una ecuación diofántica polinómica dada con coeficientes enteros tiene soluciones enteras (irresolubilidad del décimo problema de Hilbert). Sin embargo, cuando las soluciones son los puntos de una variedad abeliana, esta conjetura asegura que el tamaño del grupo de puntos racionales está relacionado con el comportamiento de una función zeta ζ(s) asociada cerca del punto s=1. En particular, asegura que si ζ(1) = 0, entonces hay infinitos puntos racionales (soluciones), y recíprocamente, si ζ(1) ≠ 0, entonces sólo existe un número finito.
Es uno de los siete problemas del milenio, cuya solución premia el Instituto Clay de Matemáticas con un millón de dólares.

Hipótesis de Poincaré

De Wikipedia, la enciclopedia libre
Saltar a: navegación, búsqueda
La Conjetura de Poincaré fue una de las hipótesis más importantes de la topología, que dejó de ser conjetura para ser un teorema tras su comprobación. El teorema sostiene que la esfera tridimensional, también llamada 3-esfera o hiperesfera, es la única variedad compacta tridimensional en la que todo lazo o círculo cerrado (1-esfera) se puede deformar (transformar) en un punto. Este último enunciado es equivalente a decir que sólo hay una variedad cerrada y simplemente conexa de dimensión 3, la esfera tridimensional.
A fecha de 2011, ha sido el único de los siete problemas del milenio en ser demostrado.

Concepto e historia

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas.
Puedes añadirlas así o avisar al autor principal del artículo en su página de discusión pegando: {{subst:Aviso referencias|Hipótesis de Poincaré}} ~~~~

La superficie de un balón de fútbol, por ejemplo, es casi un ejemplo de variedad de dimensión 2, una 2-esfera; lo podemos manipular como queramos, dándole diferentes formas, pero sin romperlo, y seguirá siendo una 2-esfera. El criterio para comprobar si una variedad es una 2-esfera es muy sencillo: imagínese una goma elástica tremendamente deformable apoyada sobre la superficie del balón; si la goma se puede comprimir (sin salirse de la superficie) hasta ocupar un solo punto, y esto en cualquier parte de la superficie, el balón es una 2-esfera y se dice que es simplemente conexa.
El problema de clasificar las variedades en el espacio usando como criterio de clasificación el concepto de homeomorfismo fue resuelto en el siglo XIX. Así, la esfera es una variedad de dimensión 2 (cada trozo pequeño de la esfera es un pequeño trozo de plano ligeramente deformado), cerrada y simplemente conexa y se estableció que toda variedad de dimensión 2, cerrada y simplemente conexa es homeomorfa a la esfera. Dicho de otro modo: sólo hay una variedad (homeomórfica) de dimensión n=2, cerrada y simplemente conexa, y se trata de la esfera (y sus homeomorfos).
Mas técnicamente, en 1904, el matemático francés Henri Poincaré (1854-1912) conjeturó que el resultado obtenido para la esfera n=2 del espacio de dimensión 3 tenía un análogo para la esfera n=3 del espacio de dimensión 4. En otras palabras, en el espacio de dimensión 4, toda variedad de dimensión n=3, cerrada y simplemente conexa, sería homeomorfa a la esfera de dimensión n=3. Pero Poincaré no consiguió probar su conjetura. Tampoco ninguno de sus contemporáneos ni sucesores. Con el tiempo, la conjetura de Poincaré cobró interés hasta convertirse en el problema abierto más notable de la Topología geométrica, con destacables implicaciones para la Física. Más aún, llegó a convertirse en uno de los problemas sin resolver más importantes de la Matemática.
Para dimensión dos ya fue demostrada en el siglo XIX. Para n=5, hubo de esperar hasta 1961, cuando lo hizo Erik Christopher Zeeman. Ese mismo año, Stephen Smale lo consiguió para n igual o mayor que 7 y, en 1962, John R. Stallings para el caso n=6. Los casos n=3 y n=4 se resistían y hubo que esperar a 1986 cuando, en lo que se consideró una hazaña matemática del estadounidense Michael Hartley Freedman, se consiguió demostrar el caso n=4. El problema es que, resuelto con éxito para todas las demás dimensiones, el caso original n=3, planteado por Poincaré, se resistía denodadamente a cualquier demostración matemática hasta que Grigori Perelmán hizo pública su demostración.
Henri Poincaré estableció dicha conjetura en 1904, indicando que la esfera tridimensional era única y que ninguna de las otras variedades tridimensionales compartían sus propiedades.

 Resolución de la Hipótesis

Grigori Perelmán resolvió la hipótesis de Poincaré. Justamente por resolver este problema, Perelman había recibido en 2006 la medalla Fields, considerada el Nobel de las matemáticas. Otro premio que también rechazó.

 Demostración de la conjetura

En un esfera-2 ordinaria, cualquier lazo se puede apretar continuamente a un punto en la superficie. ¿Esta condición caracteriza la esfera-2? La respuesta es sí, y ha sido conocida por mucho tiempo. La conjetura de Poincaré hace la misma pregunta para la más difícil de visualizar esfera-3. Grigori Perelmán probó eso de nuevo, la respuesta es sí.
El enunciado no pudo ser resuelto durante un siglo y su demostración fue considerada uno de Los siete problemas del Milenio propuestos por el Clay Mathematics Institute.
El matemático ruso Grigori Perelmán anunció haberlo hecho en 2002 a través de dos publicaciones en internet.[1]
El 5 de junio de 2006 los matemáticos chinos Zhu Xiping y Cao Huaidong anunciaron la demostración completa,[2] basándose en los trabajos preliminares de Perelman (éstos sí publicados en revistas especializadas), lo que, una vez realizada su validación por la comunidad matemática, daría fin a la clasificación completa de las estructuras topológicas de dimensión tres o tridimensionales. Sin embargo, una gran parte de la comunidad matemática piensa que la demostración corresponde a Perelman y considera el trabajo de los matemáticos chinos como un plagio. La Academia China de Ciencias, en defensa de Zhu Xiping y Cao Huaidong, afirmó que el ruso estableció las líneas generales para probar la conjetura, pero no dijo específicamente cómo resolver el enigma.
Finalmente, se reconoció el trabajo de Perelman cuando se le otorgó la Medalla Fields en el marco del XXV Congreso Internacional de Matemáticos (ICM2006) con sede en Madrid en agosto de 2006, la cual rechazó. En declaraciones a un semanario estadounidense (The New Yorker), Perelman aseguró no querer ser una mascota en el mundo de las matemáticas, estimando que no necesita otro reconocimiento sobre la validez de su trabajo.
Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)